3 绝对圆锥曲线

在进一步了解相机标定前，有必要了解绝对圆锥曲线（Absolute ）这一概念。

对于一个3D空间的点x，其投影空间的坐标为：x~=[x1,x2,x3,x4]T。我们定义无穷远处的平面用符号Π∞表示，该平面内的投影空间点坐标满足x4=0，则位于圆锥曲线Ω上的点满足：

{

x21+x22+x23=0x4=0.(1)

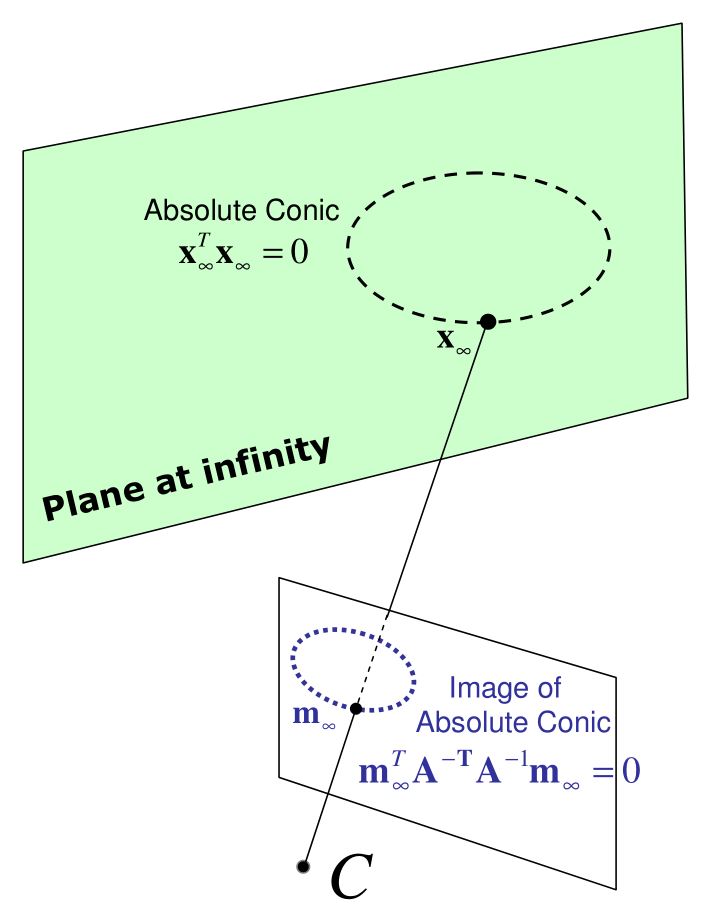
令x∞=[x1,x2,x3]T是绝对圆锥曲线Ω上的点，如上图所示。由定义可知xT∞x∞=0，同时也有x~∞=[x1,x2,x3,0]T满足x~T∞x~∞=0。读至此处，我们发现不管是Π∞和Ω，还是x∞和x~∞都是存粹想象出来的，很难在实际生活里找到实例，但是科学就是这么迷人，给定一个起始点，想象和求知探索的渴求却不受其限制，直至永无止境。

让我们再看公式(1)，如果我们令：x=x1/x3，y=x2/x3，显而易见，位于曲线Ω上的点方程就可以写成：x2+y2=−1，这就是一个圆方程，只不过我们所想象出来的这个虚拟圆的半径为−1−−−√，当然对于了解复数（）概念的我们，这并没什么不可。

此时，或许我们会困惑，为什么要费尽心机想象出绝对圆锥曲线呢？原因在于绝对圆锥曲线所具有的一条重要特性：对于刚体变换具有不变性，这么说是不是有点不明觉厉，那就继续往下看。

首先简单讲一下刚体变换：只有物体的位置（平移变换）和朝向（旋转变换）发生改变，而形状不变，得到的变换称为刚体变换。以三维刚体变换为例：

x=[R  t]X(2)

或者表述为：

x=RX+t   or   x=R(X+C)(3)

令H=[R0t1]，对于位于绝对圆锥曲线Ω上的点x~∞=[x∞0]，刚体变换后的点x~′∞可表示为：

x~′∞=Hx~∞=[Rx∞0](4)

则x′∞很明显也是位于无穷远平面上的点，而且是位于同一绝对圆锥曲线Ω上点：

x′T∞x′∞=(Rx∞)T(Rx∞)=xT∞(RTR)x∞=0(5)

令绝对圆锥曲线Ω对应的图像称为ω，也被简记为IAC（Image of the absolute conic），当然这也是想象出来的~于是对于Ω上的任一点x∞，其像点m∞满足：

m~∞=sA[R  t][x∞0]=sARx∞(6)

m~∞A−TA−1m~∞=s2xT∞RTRx∞=s2xT∞x∞=0(7)

因此，绝对圆锥曲线成像构成一个虚构曲线，并且由公式(7)可以看出，这个虚拟曲线由A−TA−1决定，这与相机的外参完全无关，而仅仅由相机内参决定。可以设想，如果我们找到了绝对圆锥曲线通过相机所成的图像，那就可以求解出相机内参。至此，我想大家也就明白为什么会提出Absolute Conic这一概念了吧。事实上，这一理论在相机自检校标定法（Self-calibration）中作为基础理论，十分重要。

后续文章将会为大家介绍几种确定绝对圆锥曲线Ω对应的图像ω的方法。